原文:http://blog.csdn.net/hengyunabc/article/details/19177877
过年红包很火,最近有个项目也要做抢红包,于是写了个红包的生成算法。
红包生成算法的需求
预先生成所有的红包还是一个请求随机生成一个红包
简单来说,就是把一个大整数m分解(直接以“分为单位,如1元即100)分解成n个小整数的过程,小整数的范围是[min, max]。
最简单的思路,先保底,每个小红包保证有min,然后每个请求都随机生成一个0到(max-min)范围的整数,再加上min就是红包的钱数。
这个算法虽然简单,但是有一个弊端:最后生成的红包可能都是min钱数的。也就是说可能最后的红包都是0.01元的。
另一种方式是预先生成所有红包,这样就比较容易控制了。我选择的是预先生成所有的红包。
理想的红包生成算法
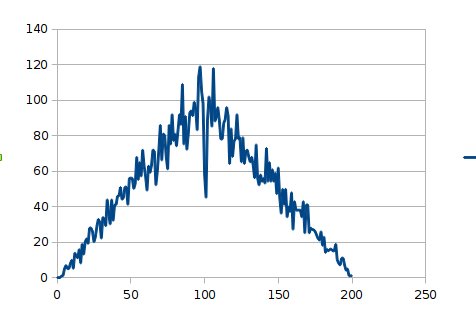
理想的红包生成结果是平均值附近的红包比较多,大红包和小红包的数量比较少。
可以想像下,生成红包的数量的分布有点像正态分布。
那么如何实现这种平均线附近值比较多的要求呢?
就是要找到一种算法,可以提高平均值附近的概率。那么利用一种”膨胀“再”收缩“的方式来达到这种效果。
先平方,再生成平方范围内的随机数,再开方,那么概率就不再是平均的了。
具体算法:
public class HongBaoAlgorithm { static Random random = new Random(); static { random.setSeed(System.currentTimeMillis()); } public static void main(String[] args) { long max = 200; long min = 1; long[] result = HongBaoAlgorithm.generate(100_0000, 10_000, max, min); long total = 0; for (int i = 0; i < result.length; i++) { // System.out.println("result[" + i + "]:" + result[i]); // System.out.println(result[i]); total += result[i]; } //检查生成的红包的总额是否正确 System.out.println("total:" + total); //统计每个钱数的红包数量,检查是否接近正态分布 int count[] = new int[(int) max + 1]; for (int i = 0; i < result.length; i++) { count[(int) result[i]] += 1; } for (int i = 0; i < count.length; i++) { System.out.println("" + i + " " + count[i]); } } /** * 生产min和max之间的随机数,但是概率不是平均的,从min到max方向概率逐渐加大。 * 先平方,然后产生一个平方值范围内的随机数,再开方,这样就产生了一种“膨胀”再“收缩”的效果。 * * @param min * @param max * @return */ static long xRandom(long min, long max) { return sqrt(nextLong(sqr(max - min))); } /** * * @param total * 红包总额 * @param count * 红包个数 * @param max * 每个小红包的最大额 * @param min * 每个小红包的最小额 * @return 存放生成的每个小红包的值的数组 */ public static long[] generate(long total, int count, long max, long min) { long[] result = new long[count]; long average = total / count; long a = average - min; long b = max - min; // //这样的随机数的概率实际改变了,产生大数的可能性要比产生小数的概率要小。 //这样就实现了大部分红包的值在平均数附近。大红包和小红包比较少。 long range1 = sqr(average - min); long range2 = sqr(max - average); for (int i = 0; i < result.length; i++) { //因为小红包的数量通常是要比大红包的数量要多的,因为这里的概率要调换过来。 //当随机数>平均值,则产生小红包 //当随机数 <平均值,则产生大红包 if (nextlong(min, max)> average) { // 在平均线上减钱// long temp = min + sqrt(nextLong(range1)); long temp = min + xRandom(min, average); result[i] = temp; total -= temp; } else { // 在平均线上加钱// long temp = max - sqrt(nextLong(range2)); long temp = max - xRandom(average, max); result[i] = temp; total -= temp; } } // 如果还有余钱,则尝试加到小红包里,如果加不进去,则尝试下一个。 while (total > 0) { for (int i = 0; i < result.length; i++) { if (total > 0 && result[i] < max) { result[i]++; total--; } } } // 如果钱是负数了,还得从已生成的小红包中抽取回来 while (total < 0) { for (int i = 0; i < result.length; i++) { if (total < 0 && result[i] > min) { result[i]--; total++; } } } return result; } static long sqrt(long n) { // 改进为查表? return (long) Math.sqrt(n); } static long sqr(long n) { // 查表快,还是直接算快? return n * n; } static long nextLong(long n) { return random.nextInt((int) n); } static long nextLong(long min, long max) { return random.nextInt((int) (max - min + 1)) + min; }}
统计了下生成的结果,还是比较符合要求的。